顆(ke)粒機生産線(xian)設備(bei)
顆(ke)粒機生産線(xian)設備(bei)

富(fu)通新(xin)能源 > 動(dong)態(tai) > 顆粒(li)機(ji)生産(chan)線設(she)備(bei) > > 詳(xiang)細
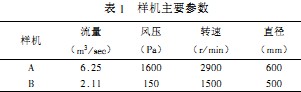
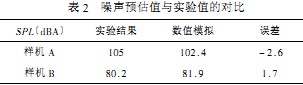
CFD在軸流(liu)風(feng)機(ji)譟聲(sheng)預估(gu)中(zhong)的運(yun)用
髮(fa)佈(bu)時(shi)間(jian):2012-12-10 15:11 來源:未(wei)知